Bài toán 3n + một là gì?

Bài toán 3n + 1, có cách gọi khác là định lý Collatz hay vấn đề Syracuse, là trong những bài toán chưa xuất hiện lời giải vào toán học. Vấn đề này được bộc lộ như sau: ban đầu với một trong những nguyên dương n, nếu n là số chẵn thì phân tách nó cho 2, nếu n là số lẻ thì nhân nó cùng với 3 rồi thêm vào đó 1. Lặp lại quá trình này cho tới khi dành được số 1. Vấn đề đưa ra là liệu số đông số nguyên dương đều sẽ sau cùng rơi vào quy trình 1, hay sẽ có được trường đúng theo ngoại lệ?

Bài toán 3n + 1 chọn cái tên theo cách làm được sử dụng trong quy trình tính toán: với ngẫu nhiên số nguyên dương nào, giả dụ là số chẵn, ta chia nó mang đến 2; nếu như là số lẻ, ta nhân với 3 và cộng thêm 1. Quá trình này tiếp tục cho tới khi số kia trở về 1. Dù đã có thử nghiệm với hàng tỷ số, nhưng cho đến nay, chưa xuất hiện ai chứng tỏ được rằng tất cả các số đều lâm vào tình thế chu trình này. Điều này khiến bài toán trở thành trong số những vấn đề mở đặc biệt quan trọng nhất trong triết lý số học.

Bạn đang xem: An 3n 1

Tên gọi khác với sự liên quan

Bài toán 3n + 1 còn theo thông tin được biết đến với tương đối nhiều tên gọi không giống nhau như việc Collatz, sự việc Syracuse, hay việc Ulam. Những chiếc tên này thường xuyên được đặt dựa trên những người đã nghiên cứu và đề xuất bài toán. Collatz, đơn vị toán học tín đồ Đức, là người đầu tiên đưa ra bài toán này vào thời điểm năm 1937. Trong những khi đó, đầy đủ nhà toán học khác như Ulam tốt Kakutani cũng có những đóng góp góp đặc trưng trong việc phân tích bài toán này.

Tình trạng giải quyết và xử lý hiện tại

Chưa có bằng chứng bác bỏ

Đến nay, việc 3n + 1 vẫn không được giải quyết và xử lý một cách chủ yếu thức. Mặc dù đã có nhiều nghiên cứu, chứng tỏ thử nghiệm và ứng dụng máy tính, mà lại vẫn chưa tồn tại ai chứng tỏ rằng toàn bộ các số nguyên dương mọi sẽ rơi vào chu trình 1. Điều này khiến cho bài toán vẫn là một trong những vấn đề mở nổi tiếng nhất trong toán học. Những nhà toán học vẫn liên tục nghiên cứu giúp và mong muốn một ngày nào đó sẽ tìm ra được giải thuật cho bài toán này.

Ứng dụng laptop trong câu hỏi kiểm tra

Ứng dụng laptop là một công cụ đặc biệt quan trọng trong việc kiểm tra tính chính xác của bài toán 3n + 1. Các máy tính tân tiến đã kiểm tra việc này với hàng nghìn số nguyên dương, và kết quả cho thấy thêm tất cả những số này các dẫn đến chu trình 1. Mặc dù nhiên, trên đây chỉ là kết quả thử nghiệm cho 1 tập hợp những số hữu hạn, và thiết yếu coi đó là chứng minh hoàn chỉnh cho tất cả các số nguyên dương. Máy vi tính chỉ giúp bọn họ kiểm tra tính đúng mực của vấn đề trên một phạm vi nhất định, nhưng không thể gắng thế chứng minh lý thuyết.

Đóng góp của các nhà toán học

Paul Erdős và đánh giá và nhận định về bài xích toán

Paul Erdős, một trong những nhà toán học nổi tiếng nhất của cụ kỷ 20, đã gồm có nhận định quan trọng về bài toán 3n + 1. Ông đến rằng đấy là một giữa những bài toán dễ dàng và đơn giản nhưng lại hết sức khó giải quyết và xử lý trong toán học. Erdős đã nhấn mạnh rằng mặc dù bài toán này dễ dàng nắm bắt và rất có thể thực hiện bằng tay, tuy vậy việc chứng minh hay bác bỏ bỏ nó lại là một thử thách cực kỳ lớn.

Jeffrey Lagarias và ý kiến về độ khó

Jeffrey Lagarias, một trong những nhà toán học hiện nay đại, đã gửi ra phần đông quan điểm sâu sắc về độ khó khăn của việc 3n + 1. Lagarias nhận định rằng bài toán này liên quan mật thiết đến triết lý số học và những vấn đề tinh vi trong kim chỉ nan đồ thị. Ông cũng đánh giá rằng việc này hoàn toàn có thể được giải quyết bằng phương pháp phát triển các phương pháp toán học tập mới, dẫu vậy điều này yên cầu một sự sáng chế và mày mò không bé dại trong nghành toán học.

Xem thêm: Lỗi Giao Dịch Không Thành Công - Nguyên Nhân và Cách Khắc Phục

Tiến triển ngay sát đây

Nghiên cứu vớt của Terence Tao và những nhà toán học khác

Terence Tao, một đơn vị toán học tập nổi tiếng, đang tham gia vào nghiên cứu và phân tích bài toán 3n + 1 và đưa ra những kết luận quan trọng. Mặc dù ông không chứng minh được việc này, nhưng nghiên cứu của Tao đã chỉ ra rằng rằng những số có thể giảm xuống một cách hối hả qua quá trình chia song hoặc nhân tía và cộng một. Điều này cho biết thêm có kỹ năng bài toán hoàn toàn có thể được giải quyết thông qua các phương pháp nghiên cứu tân tiến và sự hiểu biết sâu hơn về các chu trình trong kim chỉ nan số.

Các hiệu quả mới nhất với hướng đi tương lai

Các nghiên cứu cách đây không lâu về bài toán 3n + 1 công ty yếu triệu tập vào việc đào bới tìm kiếm ra những mô hình chu trình mới trong quá trình tính toán. Các nhà toán học tập đang nỗ lực áp dụng các phương thức như triết lý đồ thị và định hướng xác suất để tiếp cận việc này từ bỏ những khía cạnh khác nhau. Hướng đi tương lai vào việc xử lý bài toán 3n + 1 gồm thể bao gồm việc cách tân và phát triển các biện pháp toán học tập mới, cùng với việc áp dụng công nghệ tính toán tiên tiến hơn.

Ứng dụng trong thực tế và tầm quan lại trọng

Ứng dụng trong triết lý đồ thị

Bài toán 3n + 1 có thể được vận dụng trong định hướng đồ thị để mô hình hóa các chu trình. Lý thuyết đồ thị giúp chúng ta hình dung các mối quan hệ giữa những số nguyên dương và xác định xem liệu chúng có thể rơi vào quy trình 1 tuyệt không. Những áp dụng này không những giúp hiểu vấn đề một cách thâm thúy hơn mà lại còn góp sức vào những nghiên cứu triết lý trong toán học và kỹ thuật máy tính.

Tầm đặc biệt trong toán học tập và khoa học máy tính

Bài toán 3n + 1 gồm tầm đặc trưng lớn trong toán học và khoa học máy tính vì nó tương quan đến nhiều sự việc cơ bạn dạng trong định hướng số học với thuật toán. Các phương thức nghiên cứu câu hỏi này có thể giúp họ phát triển các công cụ new trong so sánh chuỗi số học, tối ưu hóa thuật toán, cùng thậm chí không ngừng mở rộng khả năng đo lường trong công nghệ máy tính. Đây là một trong ví dụ điển hình về sự việc giao trét giữa triết lý toán học tập và những ứng dụng trong thực tiễn trong technology hiện đại.

Tóm tắt câu chữ chính

Bài toán 3n + 1, tuy vậy đã được nghiên cứu và nghiên cứu và phân tích trong những thập kỷ qua, vẫn chưa tồn tại lời giải chủ yếu thức. Tuy nhiên, những nghiên cứu gần đây, nhất là của các nhà toán học tập như Terence Tao cùng Jeffrey Lagarias, đã xuất hiện thêm những phía đi new trong việc xử lý bài toán này. Mang dù chưa xuất hiện chứng minh trả chỉnh, mà lại những kết quả thử nghiệm và các ứng dụng vật dụng tính cho biết bài toán này rất có thể sẽ được xử lý trong tương lai, phụ thuộc vào những tân tiến trong toán học tập và technology tính toán.

Hướng nghiên cứu và phân tích tương lai

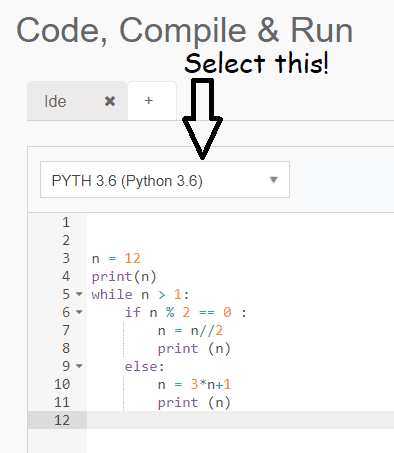
Trong tương lai, vấn đề 3n + 1 sẽ liên tiếp là giữa những thách thức lớn so với các bên toán học. Những nghiên cứu và phân tích về quy trình trong triết lý đồ thị và những công cụ giám sát và đo lường hiện đại có thể sẽ giúp bọn họ tìm ra giải mã cho bài toán này. Bên cạnh ra, bài toán còn hoàn toàn có thể giúp cải cách và phát triển thêm những phương pháp toán học mới, giao hàng cho các nghiên cứu và vận dụng trong toán học tập và khoa học máy tính.